1720-05-01 Wolff Christian-Bernoulli Johann I: Unterschied zwischen den Versionen

Aktuelle Version vom 20. Juni 2017, 07:16 Uhr

Kurzinformationen zum Brief mehr ...
Autor	Wolff, Christian, 1679-1754
Empfänger	Bernoulli, Johann I, 1667-1748
Ort	Halle
Datum	1720.05.01
Briefwechsel	Bernoulli, Johann I (1667-1748)
Signatur	Basel UB, Handschriften. SIGN: L Ia 671, Nr.18*
Fussnote	"Excerptum ex Transact. Anglio.m A. 1713 editis A. 1714 p.11 et seqq. De inventione Centri Oscillationis per Brook Taylor." 5 Blätter (15,5 x 9,5 cm), auf Blatt 3 drei Figuren

Viro Celeberrimo atque Amplissimo

Dn. Joanni Bernoullio

S. P. D.

Christianus Wolfius.

Quod negotium Cl. Filii Tui non ex voto successerit, vehementer doleo. Sed nullus dubito, quin ipsi reservata sit melior conditio. Locutus fueram cum Dn. P. Heydeno, cujus non exigua est apud Dn. de Printzen^[1] aliosque Ministros Regios autoritas: sed cur nostra consilia eventu destituta fuerint, rationem ipsimet significasti. Optarem in Nostra aut Francofurtana Academia esse Professionem, quae Cl. Filio Tuo demandari posset, tum facili negotio conficeretur, ut voti compos redderetur. Opto et spero hac de re omnia meliora. Bene fecisti, Vir Celeberrime, quod schediasmata Tua^[2] statim ad Dn. Menckenium miseris: etenim hoc pacto cessat omnis suspicio intempestivae Tuorum propalationis. Cl. Hermannus videtur utique censuram (quam vocat) Filii Tui aegre ferre: erat enim animus verbis adversus eum acerbius dictis respondendi. Mox tamen mutavit sententiam, ubi ex me intellexit, Te acerbius in Filium dicta ipsummet aegre laturum: Tuam scilicet amicitiam, quod debet, quantivis facit. Et sane nollem amicitiae vestrae per liticulas quasdam praejudicium fieri.

Me non vanum fuisse augurem de moribus Taylorianis, intellexi, ubi in Transact. Num. 360 p. 955 legis Apologiam^[3] Viri adversus Te exaratam. Sed risum tenere vix potui, ubi obscuritatem, quam ipsi objicis, excusaturus: "Sit sane", inquit, "liber ille meus^[4] nonnihil obscurus: difficile est in re fere nova et ab usu communi aliquantulum remota, non esse obscurum. Sed maxime obscurum oportet esse librum, in quem illa omnia vere dicantur (Acta Erudit A. 1718 p. 18)^[5]. Et si vere dicantur, tamen sine ulla omnino causa talia dixisse, [NB.]^[6] ab ingenuis moribus prorsus alienum est et mera contumelia."^[7] Ait itidem, Te universos Anglos indigne tractare. Te vocat Principem eorum, qui in Anglos infensi sunt et ipsum nominatim calumnia provocarunt. Unde addit: in immerentes injuria esset, in Bernoullium non est. Se Solutionem problematis de centro oscillationis cum amicis jam ab initio A. 1712 communicasse, Keilium testem invocat. Ceterum non negandum, in Transactionibus Anglicanis, quae A. 1714 pro A. 1713 prodierunt, extare hujus problematis solutionem Taylorianam^[8], quam ob obscuritatem non legi, cum jam Tuam^[9] cum voluptate atque attentione perlegissem, ubi librum obtinerem. Liber jam est in manibus bibliopegi, ut eam examinare non possim, utrum prorsus coincidat cum altera, quam in Methodo incrementorum^[10] dedit, nec ne. Suspicor fere esse diversam, quod ad eam non provocet in Apologia sua. Aggreditur in Apologia ista potissimum solutionem problematis isoperimetrici, ubi in eo est ut probet, Te calculum concinnasse et elegantiorem reddidisse in Analysi fraterna,^[11] non Tua. Omnia enim praecepta, quibus contineatur, esse fraterna. Principium Uniformitatis a se olim observatum, minime novum esse. Concludit tandem:^[12] Fortasse nunc quaeret aliquis, quo jure hic primas sibi in sublimiori illa Analysi tam obstinata ambitione arroget? ut nemo sit, qui in illa aliquid profecerit, quin continuo accusetur ad profundiora Bernoullii penetrasse. Unde constet verum esse, quod quidam nuper affirmavit,^[13] regulas extantes in libro de Analysi infinite parvorum^[14] a Bernoullio emanasse? quod laudes excellentissimi Hospitalii sint suo Praeceptori tribuendae? An hic sit idoneus, qui alias docuerit regulas differentiandi differentias? Ex his, puto, intelliges, mores Taylori non esse diversos a Keilianis.

Constitueram apertius scribere, quae mihi in principiis dynamicis aut potius demonstrationibus Hermanni non probentur; ob temporis tamen penuriam consilium mutare cogor. Et eandem ob rationem de Binaria Leibnitii Arithmetica nihil addo, nisi quod ex ore Leibnitii hauserim, Analyseos Diophanteae perfectionem per eam intendi et virum Summum in negotio etiam quadraturarum non vulgaria ab ea expectasse. Ex gemino, quem mitto, Tractatu^[15] videbis, me nunc Philosophicis meditationibus occupari. Vale et fave.

Dabam Halae Saxonum d. 1 Maji 1720.

Excerptum ex Transact. Anglic. A. 1713 editis A. 1714 p. 11 et seqq. de inventione Centri Oscillationis per Brook Taylor. ^[16]

Fussnoten

↑ Marquard Ludwig Freiherr von Printzen (1675-1725).
↑ Bernoulli, Nicolaus II Op. 116, Nic. Bernoulli Joh. Fil. Exercitatio Geometrica de Trajectoriis Orthogonalibus, continens varias earum tum inveniendarum tum construendarum methodos, sua vel Demonstratione vel Analysi munitas, cum praemissa discussione quarundam ejusdem problematis solutionum, in: AE Maji 1720, pp. 223-237; AE Suppl. Tom. VII (1721), Sect. VII, pp. 303-326; AE Suppl. Tom. VII (1721), Sect. VIII, pp. 337-353, und Bernoulli, Nicolaus II Op. 118, Responsio ad Cl. Taylori Querelas, in: Bernoulli, Nicolaus II, Enodatio alicuius Problematis Geometrici a Cel. Jac. Hermanno propositi; atque de Inveniendis Curvis Algebraicis, ab eodem Viro propositis, quae non sint indefinite rectificabiles, habeant tamen aliquos arcus rectificationem admittentes, in: AE Junii 1720, pp. 169 [recte 269]-285. Dort §.XVII-XXII, pp. 279-283. Dem Brief an Wolff war der Begleitbrief von Johann I Bernoulli an Mencke von 1720 03 27 beigelegt.
↑ Apologia D. Brook Taylor, J V D. & R S. Soc. contra V. C J. Bernoullium, Math. Prof. Basileae, in: Phil. Trans., Vol. 30, Nr. 360, March, April and May 1719, pp. 955-963.
↑ Taylor, Brook, Methodus incrementorum directa & inversa. Auctore Brook Taylor, LL. D. & Regiae Societatis Secretario, Londini (Pearson/G. Inys) 1715.
↑ Bernoulli, Joh. Bernoulli, De Solutionibus quae extant Problematum isoperimetricorum, ejusque nova eorundem problematum, aliorumque cognatorum citra calculum solvendorum methodus brevis plana & facilis, in: AE Januarii 1718, p. 18. An dieser Steller der lateinischen Erstfassung von Op. CIII spricht Johann Bernoulli positiv über Taylor als Mathematiker, rügt aber die "obscuritas" seiner Darstellung.
↑ Die eckige Klammer steht im Manuskript.
↑ Taylor, Brook, Apologia D. Brook Taylor, J V D. & R S. Soc. contra V. C J. Bernoullium, Math. Prof. Basileae, in: Phil. Trans., Vol. 30, Nr. 360, March, April and May 1719, p. 956.
↑ Taylor, Brook, De Inventione Centri Oscillationis, in: Phil. Trans., Vol. XXVIII (1713), London 1714, pp. 11-21.
↑ Bernoulli, Johann Op. CXIV, Clar. Taylori Mathematici Angli Problema Analyticum, quod omnibus Geometris non-Anglis proposuit, solutum a Joh. Bernoulli.
↑ Taylor, Brook, Methodus incrementorum directa & inversa. Auctore Brook Taylor, LL. D. & Regiae Societatis Secretario, Londini (Pearson/G. Inys), 1715.
↑ Bernoulli, Jacob Op. XCIII, Solutio propria problematis isoperimetrici propositi in Actis Lips. m. Majo 1697, p. 214, in: AE Junii 1700, pp. 261-266.
↑ Im Folgenden gibt Wolff eine Passage aus Taylor, Brook, Apologia, p. 962 wieder.
↑ Mit dem "quidam" ist wohl der Autor der Epistola pro eminente mathematico, also Johann I Bernoulli selbst gemeint.
↑ [L’Hôpital, Guillaume François Antoine de], Analyse des infiniment petits, pour l'intelligence des lignes courbes, Paris (Imprimerie Royale) 1696.
↑ Wolff, Christian, Vernünftige Gedanken von der Menschen Thun und Lassen, zu Beförderung ihrer Glückseligkeit, 1720.
↑ Auszug aus Taylor, Brook, De Inventione Centri Oscillationis, in: Phil. Trans. Vol. XXVIII (1713), London 1714, pp. 11-16.

Zurück zur gesamten Korrespondenz

[1] Marquard Ludwig Freiherr von Printzen (1675-1725).

[2] Bernoulli, Nicolaus II Op. 116, Nic. Bernoulli Joh. Fil. Exercitatio Geometrica de Trajectoriis Orthogonalibus, continens varias earum tum inveniendarum tum construendarum methodos, sua vel Demonstratione vel Analysi munitas, cum praemissa discussione quarundam ejusdem problematis solutionum, in: AE Maji 1720, pp. 223-237; AE Suppl. Tom. VII (1721), Sect. VII, pp. 303-326; AE Suppl. Tom. VII (1721), Sect. VIII, pp. 337-353, und Bernoulli, Nicolaus II Op. 118, Responsio ad Cl. Taylori Querelas, in: Bernoulli, Nicolaus II, Enodatio alicuius Problematis Geometrici a Cel. Jac. Hermanno propositi; atque de Inveniendis Curvis Algebraicis, ab eodem Viro propositis, quae non sint indefinite rectificabiles, habeant tamen aliquos arcus rectificationem admittentes, in: AE Junii 1720, pp. 169 [recte 269]-285. Dort §.XVII-XXII, pp. 279-283. Dem Brief an Wolff war der Begleitbrief von Johann I Bernoulli an Mencke von 1720 03 27 beigelegt.

[3] Apologia D. Brook Taylor, J V D. & R S. Soc. contra V. C J. Bernoullium, Math. Prof. Basileae, in: Phil. Trans., Vol. 30, Nr. 360, March, April and May 1719, pp. 955-963.

[4] Taylor, Brook, Methodus incrementorum directa & inversa. Auctore Brook Taylor, LL. D. & Regiae Societatis Secretario, Londini (Pearson/G. Inys) 1715.

[5] Bernoulli, Joh. Bernoulli, De Solutionibus quae extant Problematum isoperimetricorum, ejusque nova eorundem problematum, aliorumque cognatorum citra calculum solvendorum methodus brevis plana & facilis, in: AE Januarii 1718, p. 18. An dieser Steller der lateinischen Erstfassung von Op. CIII spricht Johann Bernoulli positiv über Taylor als Mathematiker, rügt aber die "obscuritas" seiner Darstellung.

[6] Die eckige Klammer steht im Manuskript.

[7] Taylor, Brook, Apologia D. Brook Taylor, J V D. & R S. Soc. contra V. C J. Bernoullium, Math. Prof. Basileae, in: Phil. Trans., Vol. 30, Nr. 360, March, April and May 1719, p. 956.

[8] Taylor, Brook, De Inventione Centri Oscillationis, in: Phil. Trans., Vol. XXVIII (1713), London 1714, pp. 11-21.

[9] Bernoulli, Johann Op. CXIV, Clar. Taylori Mathematici Angli Problema Analyticum, quod omnibus Geometris non-Anglis proposuit, solutum a Joh. Bernoulli.

[10] Taylor, Brook, Methodus incrementorum directa & inversa. Auctore Brook Taylor, LL. D. & Regiae Societatis Secretario, Londini (Pearson/G. Inys), 1715.

[11] Bernoulli, Jacob Op. XCIII, Solutio propria problematis isoperimetrici propositi in Actis Lips. m. Majo 1697, p. 214, in: AE Junii 1700, pp. 261-266.

[12] Im Folgenden gibt Wolff eine Passage aus Taylor, Brook, Apologia, p. 962 wieder.

[13] Mit dem "quidam" ist wohl der Autor der Epistola pro eminente mathematico, also Johann I Bernoulli selbst gemeint.

[14] [L’Hôpital, Guillaume François Antoine de], Analyse des infiniment petits, pour l'intelligence des lignes courbes, Paris (Imprimerie Royale) 1696.

[15] Wolff, Christian, Vernünftige Gedanken von der Menschen Thun und Lassen, zu Beförderung ihrer Glückseligkeit, 1720.

[16] Auszug aus Taylor, Brook, De Inventione Centri Oscillationis, in: Phil. Trans. Vol. XXVIII (1713), London 1714, pp. 11-16.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

@@ Zeile 5: / Zeile 5: @@
 <!-- Begin Bilder -->
 {|border="0"
-|<html><a href="http://www.ub.unibas.ch/digi/a100/diverse_projekte/bernoulli-jpg/IBB_5_57830_001r.jpg" target="_new"><img src="http://www.ub.unibas.ch/digi/a100/diverse_projekte/bernoulli-jpg/thumb/IBB_5_57830_001r.jpg" alt="Briefseite" title="Briefseite" /></a> &nbsp;</html>
+|<html><a href="http://www.ub.unibas.ch/digi/bez/bernoullibriefe/jpg/bernoulli-jpg/BAU_5_000057830_001r.jpg" target="_new"><img src="http://www.ub.unibas.ch/digi/bez/bernoullibriefe/jpg/bernoulli-jpg/thumb/BAU_5_000057830_001r.jpg" alt="Briefseite" title="Briefseite" /></a> &nbsp;</html>
-|<html><a href="http://www.ub.unibas.ch/digi/a100/diverse_projekte/bernoulli-jpg/IBB_5_57830_001v.jpg" target="_new"><img src="http://www.ub.unibas.ch/digi/a100/diverse_projekte/bernoulli-jpg/thumb/IBB_5_57830_001v.jpg" alt="Briefseite" title="Briefseite" /></a> &nbsp;</html>
+|<html><a href="http://www.ub.unibas.ch/digi/bez/bernoullibriefe/jpg/bernoulli-jpg/BAU_5_000057830_001v.jpg" target="_new"><img src="http://www.ub.unibas.ch/digi/bez/bernoullibriefe/jpg/bernoulli-jpg/thumb/BAU_5_000057830_001v.jpg" alt="Briefseite" title="Briefseite" /></a> &nbsp;</html>
-|<html><a href="http://www.ub.unibas.ch/digi/a100/diverse_projekte/bernoulli-jpg/IBB_5_57830_002r.jpg" target="_new"><img src="http://www.ub.unibas.ch/digi/a100/diverse_projekte/bernoulli-jpg/thumb/IBB_5_57830_002r.jpg" alt="Briefseite" title="Briefseite" /></a> &nbsp;</html>
+|<html><a href="http://www.ub.unibas.ch/digi/bez/bernoullibriefe/jpg/bernoulli-jpg/BAU_5_000057830_002r.jpg" target="_new"><img src="http://www.ub.unibas.ch/digi/bez/bernoullibriefe/jpg/bernoulli-jpg/thumb/BAU_5_000057830_002r.jpg" alt="Briefseite" title="Briefseite" /></a> &nbsp;</html>
-|<html><a href="http://www.ub.unibas.ch/digi/a100/diverse_projekte/bernoulli-jpg/IBB_5_57830_002v.jpg" target="_new"><img src="http://www.ub.unibas.ch/digi/a100/diverse_projekte/bernoulli-jpg/thumb/IBB_5_57830_002v.jpg" alt="Briefseite" title="Briefseite" /></a> &nbsp;</html>
+|<html><a href="http://www.ub.unibas.ch/digi/bez/bernoullibriefe/jpg/bernoulli-jpg/BAU_5_000057830_002v.jpg" target="_new"><img src="http://www.ub.unibas.ch/digi/bez/bernoullibriefe/jpg/bernoulli-jpg/thumb/BAU_5_000057830_002v.jpg" alt="Briefseite" title="Briefseite" /></a> &nbsp;</html>
-|<html><a href="http://www.ub.unibas.ch/digi/a100/diverse_projekte/bernoulli-jpg/IBB_5_57830_003r.jpg" target="_new"><img src="http://www.ub.unibas.ch/digi/a100/diverse_projekte/bernoulli-jpg/thumb/IBB_5_57830_003r.jpg" alt="Briefseite" title="Briefseite" /></a> &nbsp;</html>
+|<html><a href="http://www.ub.unibas.ch/digi/bez/bernoullibriefe/jpg/bernoulli-jpg/BAU_5_000057830_003r.jpg" target="_new"><img src="http://www.ub.unibas.ch/digi/bez/bernoullibriefe/jpg/bernoulli-jpg/thumb/BAU_5_000057830_003r.jpg" alt="Briefseite" title="Briefseite" /></a> &nbsp;</html>
-|<html><a href="http://www.ub.unibas.ch/digi/a100/diverse_projekte/bernoulli-jpg/IBB_5_57830_003v.jpg" target="_new"><img src="http://www.ub.unibas.ch/digi/a100/diverse_projekte/bernoulli-jpg/thumb/IBB_5_57830_003v.jpg" alt="Briefseite" title="Briefseite" /></a> &nbsp;</html>
+|<html><a href="http://www.ub.unibas.ch/digi/bez/bernoullibriefe/jpg/bernoulli-jpg/BAU_5_000057830_003v.jpg" target="_new"><img src="http://www.ub.unibas.ch/digi/bez/bernoullibriefe/jpg/bernoulli-jpg/thumb/BAU_5_000057830_003v.jpg" alt="Briefseite" title="Briefseite" /></a> &nbsp;</html>
-|<html><a href="http://www.ub.unibas.ch/digi/a100/diverse_projekte/bernoulli-jpg/IBB_5_57830_004r.jpg" target="_new"><img src="http://www.ub.unibas.ch/digi/a100/diverse_projekte/bernoulli-jpg/thumb/IBB_5_57830_004r.jpg" alt="Briefseite" title="Briefseite" /></a> &nbsp;</html>
+|<html><a href="http://www.ub.unibas.ch/digi/bez/bernoullibriefe/jpg/bernoulli-jpg/BAU_5_000057830_004r.jpg" target="_new"><img src="http://www.ub.unibas.ch/digi/bez/bernoullibriefe/jpg/bernoulli-jpg/thumb/BAU_5_000057830_004r.jpg" alt="Briefseite" title="Briefseite" /></a> &nbsp;</html>
-|<html><a href="http://www.ub.unibas.ch/digi/a100/diverse_projekte/bernoulli-jpg/IBB_5_57830_004v.jpg" target="_new"><img src="http://www.ub.unibas.ch/digi/a100/diverse_projekte/bernoulli-jpg/thumb/IBB_5_57830_004v.jpg" alt="Briefseite" title="Briefseite" /></a> &nbsp;</html>
+|<html><a href="http://www.ub.unibas.ch/digi/bez/bernoullibriefe/jpg/bernoulli-jpg/BAU_5_000057830_004v.jpg" target="_new"><img src="http://www.ub.unibas.ch/digi/bez/bernoullibriefe/jpg/bernoulli-jpg/thumb/BAU_5_000057830_004v.jpg" alt="Briefseite" title="Briefseite" /></a> &nbsp;</html>
 |-
-|<html><a href="http://www.ub.unibas.ch/digi/a100/diverse_projekte/bernoulli-jpg/IBB_5_57830_005r.jpg" target="_new"><img src="http://www.ub.unibas.ch/digi/a100/diverse_projekte/bernoulli-jpg/thumb/IBB_5_57830_005r.jpg" alt="Briefseite" title="Briefseite" /></a> &nbsp;</html>
+|<html><a href="http://www.ub.unibas.ch/digi/bez/bernoullibriefe/jpg/bernoulli-jpg/BAU_5_000057830_005r.jpg" target="_new"><img src="http://www.ub.unibas.ch/digi/bez/bernoullibriefe/jpg/bernoulli-jpg/thumb/BAU_5_000057830_005r.jpg" alt="Briefseite" title="Briefseite" /></a> &nbsp;</html>
-|<html><a href="http://www.ub.unibas.ch/digi/a100/diverse_projekte/bernoulli-jpg/IBB_5_57830_005v.jpg" target="_new"><img src="http://www.ub.unibas.ch/digi/a100/diverse_projekte/bernoulli-jpg/thumb/IBB_5_57830_005v.jpg" alt="Briefseite" title="Briefseite" /></a> &nbsp;</html>
+|<html><a href="http://www.ub.unibas.ch/digi/bez/bernoullibriefe/jpg/bernoulli-jpg/BAU_5_000057830_005v.jpg" target="_new"><img src="http://www.ub.unibas.ch/digi/bez/bernoullibriefe/jpg/bernoulli-jpg/thumb/BAU_5_000057830_005v.jpg" alt="Briefseite" title="Briefseite" /></a> &nbsp;</html>
-|<html><a href="http://www.ub.unibas.ch/digi/a100/diverse_projekte/bernoulli-jpg/IBB_5_57830_006r.jpg" target="_new"><img src="http://www.ub.unibas.ch/digi/a100/diverse_projekte/bernoulli-jpg/thumb/IBB_5_57830_006r.jpg" alt="Briefseite" title="Briefseite" /></a> &nbsp;</html>
+|<html><a href="http://www.ub.unibas.ch/digi/bez/bernoullibriefe/jpg/bernoulli-jpg/BAU_5_000057830_006r.jpg" target="_new"><img src="http://www.ub.unibas.ch/digi/bez/bernoullibriefe/jpg/bernoulli-jpg/thumb/BAU_5_000057830_006r.jpg" alt="Briefseite" title="Briefseite" /></a> &nbsp;</html>
-|<html><a href="http://www.ub.unibas.ch/digi/a100/diverse_projekte/bernoulli-jpg/IBB_5_57830_006v.jpg" target="_new"><img src="http://www.ub.unibas.ch/digi/a100/diverse_projekte/bernoulli-jpg/thumb/IBB_5_57830_006v.jpg" alt="Briefseite" title="Briefseite" /></a> &nbsp;</html>
+|<html><a href="http://www.ub.unibas.ch/digi/bez/bernoullibriefe/jpg/bernoulli-jpg/BAU_5_000057830_006v.jpg" target="_new"><img src="http://www.ub.unibas.ch/digi/bez/bernoullibriefe/jpg/bernoulli-jpg/thumb/BAU_5_000057830_006v.jpg" alt="Briefseite" title="Briefseite" /></a> &nbsp;</html>
-|<html><a href="http://www.ub.unibas.ch/digi/a100/diverse_projekte/bernoulli-jpg/IBB_5_57830_007r.jpg" target="_new"><img src="http://www.ub.unibas.ch/digi/a100/diverse_projekte/bernoulli-jpg/thumb/IBB_5_57830_007r.jpg" alt="Briefseite" title="Briefseite" /></a> &nbsp;</html>
+|<html><a href="http://www.ub.unibas.ch/digi/bez/bernoullibriefe/jpg/bernoulli-jpg/BAU_5_000057830_007r.jpg" target="_new"><img src="http://www.ub.unibas.ch/digi/bez/bernoullibriefe/jpg/bernoulli-jpg/thumb/BAU_5_000057830_007r.jpg" alt="Briefseite" title="Briefseite" /></a> &nbsp;</html>
-|<html><a href="http://www.ub.unibas.ch/digi/a100/diverse_projekte/bernoulli-jpg/IBB_5_57830_007v.jpg" target="_new"><img src="http://www.ub.unibas.ch/digi/a100/diverse_projekte/bernoulli-jpg/thumb/IBB_5_57830_007v.jpg" alt="Briefseite" title="Briefseite" /></a> &nbsp;</html>
+|<html><a href="http://www.ub.unibas.ch/digi/bez/bernoullibriefe/jpg/bernoulli-jpg/BAU_5_000057830_007v.jpg" target="_new"><img src="http://www.ub.unibas.ch/digi/bez/bernoullibriefe/jpg/bernoulli-jpg/thumb/BAU_5_000057830_007v.jpg" alt="Briefseite" title="Briefseite" /></a> &nbsp;</html>
 |}
 <!-- End Bilder -->
@@ Zeile 32: / Zeile 32: @@
 |Datum=1720.05.01
 |Briefwechsel=Bernoulli, Johann I (1667-1748)
-|Signatur=BS UB, Handschriften. SIGN: L I a 671, Nr.18*
+|Signatur=Basel UB, Handschriften. SIGN: L Ia 671, Nr.18*
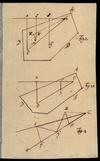
-|Fussnote=Beilage: "Excerptum ex Transact. Anglio.m A. 1713 editis A. 1714 p.11 et seqq. De inventione Centri Oscillationis per Brook Taylor." 5 Blätter (15,5 x 9,5 cm), auf Blatt 3 drei Figuren}}
+|Fussnote="Excerptum ex Transact. Anglio.m A. 1713 editis A. 1714 p.11 et seqq. De inventione Centri Oscillationis per Brook Taylor." 5 Blätter (15,5 x 9,5 cm), auf Blatt 3 drei Figuren}}
 <br style="clear:both" />
@@ Zeile 39: / Zeile 39: @@
 <!-- Begin Transkription -->
-[[File:file_icon.gif|link=http://www.ub.unibas.ch/digi/a100/diverse_projekte/bernoulli-jpg/IBB_5_57830_001r.jpg]] Viro Celeberrimo atque Amplissimo
+[[File:file_icon.gif|link=http://www.ub.unibas.ch/digi/bez/bernoullibriefe/jpg/bernoulli-jpg/BAU_5_000057830_001r.jpg]] Viro Celeberrimo atque Amplissimo
 Dn. Joanni Bernoullio
@@ Zeile 47: / Zeile 47: @@
 Christianus Wolfius.
-Quod negotium Cl. Filii Tui non ex voto successerit, vehementer doleo. Sed nullus dubito, quin ipsi reservata sit melior conditio. Locutus fueram cum Dn. P. Heydeno, cujus non exigua est apud Dn. de Printzen aliosque Ministros Regios autoritas: sed cur nostra consilia eventu destituta fuerint, rationem ipsimet significasti. Optarem in Nostra aut Francofurtana Academia esse Professionem, quae Cl. Filio Tuo demandari posset, tum facili negotio conficeretur, ut voti compos redderetur. Opto et spero hac de re omnia meliora. Bene fecisti, Vir Celeberrime, quod schediasmata Tua<ref>Bernoulli, Nicolaus II Op. 116, ''Nic. Bernoulli Joh. Fil. Exercitatio Geometrica de Trajectoriis Orthogonalibus, continens varias earum tum inveniendarum tum construendarum methodos, sua vel Demonstratione vel Analysi munitas, cum praemissa discussione quarundam ejusdem problematis solutionum'': AE Maji 1720, pp. 223-237; AE Suppl. Tom. VII (1721), Sect. VII, pp. 303-326; AE Suppl. Tom. VII (1721), Sect. VIII, pp. 337-353, und Bernoulli, Nicolaus II Op. 118, ''Responsio ad Cl. Taylori Querelas, §.XVII-XXII, pp. 279-283 in: Enodatio alicuius Problematis Geometrici a Cel. Jac. Hermanno propositi; atque de Inveniendis Curvis Algebraicis, ab eodem Viro propositis, quae non sint indefinite rectificabiles, habeant tamen aliquos arcus rectificationem admittentes. Per Nic. Bernoulli Jo. Fil.'': AE Junii 1720, pp. 169 [recte 269]-285. Dem Brief an Wolff war der Begleitbrief von Johann I Bernoulli an Mencke von 1720 03 27 beigelegt.</ref> statim ad Dn. Menckenium miseris: etenim hoc pacto cessat omnis suspicio intempestivae Tuorum propalationis. Cl. Hermannus videtur utique censuram (quam vocat) Filii Tui aegre ferre: erat enim animus verbis adversus eum acerbius dictis respondendi. Mox tamen mutavit sententiam, ubi ex me intellexit, Te acerbius in Filium dicta ipsummet aegre laturum: Tuam scilicet amicitiam, quod debet, quantivis facit. Et sane nollem amicitiae vestrae per liticulas quasdam praejudicium fieri.
+Quod negotium Cl. Filii Tui non ex voto successerit, vehementer doleo. Sed nullus dubito, quin ipsi reservata sit melior conditio. Locutus fueram cum Dn. P. Heydeno, cujus non exigua est apud Dn. de Printzen<ref>Marquard Ludwig Freiherr von Printzen (1675-1725).</ref> aliosque Ministros Regios autoritas: sed cur nostra consilia eventu destituta fuerint, rationem ipsimet significasti. Optarem in Nostra aut Francofurtana Academia esse Professionem, quae Cl. Filio Tuo demandari posset, tum facili negotio conficeretur, ut voti compos redderetur. Opto et spero hac de re omnia meliora. Bene fecisti, Vir Celeberrime, quod schediasmata Tua<ref>Bernoulli, Nicolaus II Op. 116, ''Nic. Bernoulli Joh. Fil. Exercitatio Geometrica de Trajectoriis Orthogonalibus, continens varias earum tum inveniendarum tum construendarum methodos, sua vel Demonstratione vel Analysi munitas, cum praemissa discussione quarundam ejusdem problematis solutionum'', in: AE Maji 1720, pp. 223-237; AE Suppl. Tom. VII (1721), Sect. VII, pp. 303-326; AE Suppl. Tom. VII (1721), Sect. VIII, pp. 337-353, und Bernoulli, Nicolaus II [http://www.ub.unibas.ch/bernoulli/index.php/Werkverzeichnisjohib#Op._118_.7Bpubl._von_Nic._II_B..7D_Responsio_ad_Cl._Taylori_Querelas Op. 118], ''Responsio ad Cl. Taylori Querelas'', in: Bernoulli, Nicolaus II, ''Enodatio alicuius Problematis Geometrici a Cel. Jac. Hermanno propositi; atque de Inveniendis Curvis Algebraicis, ab eodem Viro propositis, quae non sint indefinite rectificabiles, habeant tamen aliquos arcus rectificationem admittentes'', in: AE Junii 1720, pp. 169 [recte 269]-285. Dort §.XVII-XXII, pp. 279-283. Dem Brief an Wolff war der Begleitbrief von Johann I Bernoulli an Mencke von 1720 03 27 beigelegt.</ref> statim ad Dn. Menckenium miseris: etenim hoc pacto cessat omnis suspicio intempestivae Tuorum propalationis. Cl. Hermannus videtur utique censuram (quam vocat) Filii Tui aegre ferre: erat enim animus verbis adversus eum acerbius dictis respondendi. Mox tamen mutavit sententiam, ubi ex me intellexit, Te acerbius in Filium dicta ipsummet aegre laturum: Tuam scilicet amicitiam, quod debet, quantivis facit. Et sane nollem amicitiae vestrae per liticulas quasdam praejudicium fieri.
-Me non vanum fuisse augurem de moribus Taylorianis, intellexi, ubi in Transact. Num. 360 p. 955 legis Apologiam<ref>''Apologia D. Brook Taylor, J V D. & R S. Soc. contra V. C J. Bernoullium, Math. Prof. Basileae'', in: Phil. Trans. , Vol. 30, Nr. 360, March, April and May 1719, pp. 955-963</ref> Viri adversus Te exaratam. Sed risum tenere vix potui, ubi obscuritatem, quam ipsi objicis, excusaturus: "Sit sane", inquit, "liber ille meus<ref>Taylor, Brook, ''Methodus Incrementorum Directa & Inversa'', Londini 1715</ref> [[File:file_icon.gif|link=http://www.ub.unibas.ch/digi/a100/diverse_projekte/bernoulli-jpg/IBB_5_57830_001v.jpg]] nonnihil obscurus: difficile est in re fere nova et ab usu communi aliquantulum remota, non esse obscurum. Sed maxime obscurum oportet esse librum, in quem illa omnia vere dicantur (Acta Erudit A. 1718 p. 18.)<ref>Johann I Bernoulli Op. xxx, De solutionibus ...</ref>. Et si vere dicantur, tamen sine ulla omnino causa talia dixisse, [NB.]<ref>Die eckige Klammer steht im Manuskript</ref> ab ingenuis moribus prorsus alienum est et mera contumelia."<ref>''Apologia D. Brook Taylor, J V D. & R S. Soc. contra V. C J. Bernoullium, Math. Prof. Basileae'', in: Phil. Trans. , Vol. 30, Nr. 360, March, April and May 1719, p. 956.</ref> Ait itidem, Te universos Anglos indigne tractare. Te vocat Principem eorum, qui in Anglos infensi sunt et ipsum nominatim calumnia provocarunt. Unde addit: in immerentes injuria esset, in Bernoullium non est. Se Solutionem problematis de centro oscillationis cum amicis jam ab initio A. 1712 communicasse, Keilium testem invocat. Ceterum non negandum, in Transactionibus Anglicanis, quae A. 1714 pro A. 1713 prodierunt, extare hujus problematis solutionem Taylorianam<ref>Taylor, Brook, ''De Inventione Centri Oscillationis'': Phil. Trans. Vol. XXVIII (1713), London 1714, pp. 11-21</ref>, quam ob obscuritatem non legi, cum jam Tuam<ref>Joh. I B. Op. CXIV, ''Clar. Taylori Mathematici Angli Problema Analyticum, quod omnibus Geometris non-Anglis proposuit, solutum a Joh. Bernoulli'': AE Junii 1719, pp. 256-270</ref> cum voluptate atque attentione perlegissem, ubi librum obtinerem. Liber jam est in manibus bibliopegi, ut eam examinare non possim, utrum prorsus coincidat cum altera, quam in Methodo incrementorum<ref>Taylor, Brook, ''Methodus Incrementorum Directa & Inversa'', Londini 1715</ref> dedit, nec ne. Suspicor fere esse diversam, quod ad eam non provocet in Apologia sua. Aggreditur in Apologia ista potissimum solutionem problematis isoperimetrici, ubi in eo est ut probet, Te calculum concinnasse et elegantiorem reddidisse in Analysi fraterna,<ref>Bernoulli, Jacob Op. XCIII, ''Solutio propria problematis isoperimetrici propositi in Actis Lips. m. Majo 1697, p. 214'': AE Junii 1700, pp. 261-266</ref> non Tua. Omnia enim praecepta, quibus contineatur, esse fraterna. Principium Uniformitatis a se olim observatum, minime novum esse. Concludit tandem: Fortasse nunc quaeret aliquis, quo jure hic primas sibi in sublimiori illa Analysi tam obstinata ambitione arroget? ut nemo sit, qui in illa aliquid profecerit, quin continuo accusetur ad profundiora Bernoullii penetrasse. Unde constet verum esse, quod quidam nuper affirmavit,<ref>Mit dem "quidam" ist wohl der Autor der ''Epistola pro eminente mathematico'', also Johann I Bernoulli selbst gemeint.</ref> regulas extantes in libro de Analysi infinite parvorum<ref>L'Hôpital, Guillaume-François Antoine de, ''Analyse des infiniment petits, Pour l'intelligence des lignes courbes'', Paris 1696</ref> a Bernoullio emanasse? quod laudes excellentissimi Hospitalii sint suo Praeceptori tribuendae? An hic sit idoneus, qui alias docuerit regulas differentiandi differentias?<ref>Diese von Wolff zitierte Passage findet sich in: Taylor, Brook, ''Apologia'', Op. cit., p. 962</ref> Ex his, puto, intelliges, mores Taylori non esse diversos a Keilianis.
+Me non vanum fuisse augurem de moribus Taylorianis, intellexi, ubi in Transact. Num. 360 p. 955 legis Apologiam<ref>''Apologia D. Brook Taylor, J V D. & R S. Soc. contra V. C J. Bernoullium, Math. Prof. Basileae'', in: Phil. Trans., Vol. 30, Nr. 360, March, April and May 1719, pp. 955-963.</ref> Viri adversus Te exaratam. Sed risum tenere vix potui, ubi obscuritatem, quam ipsi objicis, excusaturus: "Sit sane", inquit, "liber ille meus<ref>Taylor, Brook, ''Methodus incrementorum directa & inversa. Auctore Brook Taylor, LL. D. & Regiae Societatis Secretario'', Londini (Pearson/G. Inys) 1715.</ref> [[File:file_icon.gif|link=http://www.ub.unibas.ch/digi/bez/bernoullibriefe/jpg/bernoulli-jpg/BAU_5_000057830_001v.jpg]] nonnihil obscurus: difficile est in re fere nova et ab usu communi aliquantulum remota, non esse obscurum. Sed maxime obscurum oportet esse librum, in quem illa omnia vere dicantur (Acta Erudit A. 1718 p. 18)<ref>Bernoulli, Joh. Bernoulli, ''De Solutionibus quae extant Problematum isoperimetricorum, ejusque nova eorundem problematum, aliorumque cognatorum citra calculum solvendorum methodus brevis plana & facilis'', in: AE Januarii 1718, p. 18. An dieser Steller der lateinischen Erstfassung von Op. CIII spricht Johann Bernoulli positiv über Taylor als Mathematiker, rügt aber die "obscuritas" seiner Darstellung.</ref>. Et si vere dicantur, tamen sine ulla omnino causa talia dixisse, [NB.]<ref>Die eckige Klammer steht im Manuskript.</ref> ab ingenuis moribus prorsus alienum est et mera contumelia."<ref>Taylor, Brook, ''Apologia D. Brook Taylor, J V D. & R S. Soc. contra V. C J. Bernoullium, Math. Prof. Basileae'', in: Phil. Trans., Vol. 30, Nr. 360, March, April and May 1719, p. 956.</ref> Ait itidem, Te universos Anglos indigne tractare. Te vocat Principem eorum, qui in Anglos infensi sunt et ipsum nominatim calumnia provocarunt. Unde addit: in immerentes injuria esset, in Bernoullium non est. Se Solutionem problematis de centro oscillationis cum amicis jam ab initio A. 1712 communicasse, Keilium testem invocat. Ceterum non negandum, in Transactionibus Anglicanis, quae A. 1714 pro A. 1713 prodierunt, extare hujus problematis solutionem Taylorianam<ref>Taylor, Brook, ''De Inventione Centri Oscillationis'', in: Phil. Trans., Vol. XXVIII (1713), London 1714, pp. 11-21.</ref>, quam ob obscuritatem non legi, cum jam Tuam<ref>Bernoulli, Johann [http://www.ub.unibas.ch/bernoulli/index.php/Werkverzeichnisjohib#Op._CXIV_Clar._Taylori_Mathematici_Angli_Problema_Analyticum_..._solutum_a_Joh._Bernoulli Op. CXIV], ''Clar. Taylori Mathematici Angli Problema Analyticum, quod omnibus Geometris non-Anglis proposuit, solutum a Joh. Bernoulli''.</ref> cum voluptate atque attentione perlegissem, ubi librum obtinerem. Liber jam est in manibus bibliopegi, ut eam examinare non possim, utrum prorsus coincidat cum altera, quam in Methodo incrementorum<ref>Taylor, Brook, ''Methodus incrementorum directa & inversa. Auctore Brook Taylor, LL. D. & Regiae Societatis Secretario'', Londini (Pearson/G. Inys), 1715.</ref> dedit, nec ne. Suspicor fere esse diversam, quod ad eam non provocet in Apologia sua. Aggreditur in Apologia ista potissimum solutionem problematis isoperimetrici, ubi in eo est ut probet, Te calculum concinnasse et elegantiorem reddidisse in Analysi fraterna,<ref>Bernoulli, Jacob Op. XCIII, ''Solutio propria problematis isoperimetrici propositi in Actis Lips. m. Majo 1697, p. 214'', in: AE Junii 1700, pp. 261-266.</ref> non Tua. Omnia enim praecepta, quibus contineatur, esse fraterna. Principium Uniformitatis a se olim observatum, minime novum esse. Concludit tandem:<ref>Im Folgenden gibt Wolff eine Passage aus Taylor, Brook, ''Apologia'', p. 962 wieder.</ref> Fortasse nunc quaeret aliquis, quo jure hic primas sibi in sublimiori illa Analysi tam obstinata ambitione arroget? ut nemo sit, qui in illa aliquid profecerit, quin continuo accusetur ad profundiora Bernoullii penetrasse. Unde constet verum esse, quod quidam nuper affirmavit,<ref>Mit dem "quidam" ist wohl der Autor der ''Epistola pro eminente mathematico'', also Johann I Bernoulli selbst gemeint.</ref> regulas extantes in libro de Analysi infinite parvorum<ref>[L’Hôpital, Guillaume François Antoine de], ''Analyse des infiniment petits, pour l'intelligence des lignes courbes'', Paris (Imprimerie Royale) 1696.</ref> a Bernoullio emanasse? quod laudes excellentissimi Hospitalii sint suo Praeceptori tribuendae? An hic sit idoneus, qui alias docuerit regulas differentiandi differentias? Ex his, puto, intelliges, mores Taylori non esse diversos a Keilianis.
-[[File:file_icon.gif|link=http://www.ub.unibas.ch/digi/a100/diverse_projekte/bernoulli-jpg/IBB_5_57830_002r.jpg]] Constitueram apertius scribere, quae mihi in principiis dynamicis aut potius demonstrationibus Hermanni non probentur; ob temporis tamen penuriam consilium mutare cogor. Et eandem ob rationem de Binaria Leibnitii Arithmetica nihil addo, nisi quod ex ore Leibnitii hauserim, Analyseos Diophanteae perfectionem per eam intendi et virum Summum in negotio etiam quadraturarum non vulgaria ab ea expectasse. Ex gemino, quem mitto, Tractatu<ref>Wolff, Christian, ''Vernünftige Gedanken von der Menschen Thun und Lassen, zu Beförderung ihrer Glückseligkeit'', 1720 </ref> videbis, me nunc Philosophicis meditationibus occupari. Vale et fave.
+[[File:file_icon.gif|link=http://www.ub.unibas.ch/digi/bez/bernoullibriefe/jpg/bernoulli-jpg/BAU_5_000057830_002r.jpg]] Constitueram apertius scribere, quae mihi in principiis dynamicis aut potius demonstrationibus Hermanni non probentur; ob temporis tamen penuriam consilium mutare cogor. Et eandem ob rationem de Binaria Leibnitii Arithmetica nihil addo, nisi quod ex ore Leibnitii hauserim, Analyseos Diophanteae perfectionem per eam intendi et virum Summum in negotio etiam quadraturarum non vulgaria ab ea expectasse. Ex gemino, quem mitto, Tractatu<ref>Wolff, Christian, ''Vernünftige Gedanken von der Menschen Thun und Lassen, zu Beförderung ihrer Glückseligkeit'', 1720.</ref> videbis, me nunc Philosophicis meditationibus occupari. Vale et fave.
 Dabam Halae Saxonum d. 1 Maji 1720.
-[[File:file_icon.gif|link=http://www.ub.unibas.ch/digi/a100/diverse_projekte/bernoulli-jpg/IBB_5_57830_003r.jpg]] Excerptum ex Transact. Anglic. A. 1713 editis A. 1714 p. 11 et seqq. de inventione Centri Oscillationis per Brook Taylor. <ref>Die Vorlage des Exzerpts findet sich dort auf pp. 11-16</ref>
+[[File:file_icon.gif|link=http://www.ub.unibas.ch/digi/bez/bernoullibriefe/jpg/bernoulli-jpg/BAU_5_000057830_003r.jpg]] Excerptum ex Transact. Anglic. A. 1713 editis A. 1714 p. 11 et seqq. de inventione Centri Oscillationis per Brook Taylor. <ref>Auszug aus Taylor, Brook, ''De Inventione Centri Oscillationis'', in: Phil. Trans. Vol. XXVIII (1713), London 1714, pp. 11-16.</ref>
-[[File:file_icon.gif|link=http://www.ub.unibas.ch/digi/a100/diverse_projekte/bernoulli-jpg/IBB_5_57830_003r.jpg]] [[File:file_icon.gif|link=http://www.ub.unibas.ch/digi/a100/diverse_projekte/bernoulli-jpg/IBB_5_57830_003v.jpg]] [[File:file_icon.gif|link=http://www.ub.unibas.ch/digi/a100/diverse_projekte/bernoulli-jpg/IBB_5_57830_004r.jpg]] [[File:file_icon.gif|link=http://www.ub.unibas.ch/digi/a100/diverse_projekte/bernoulli-jpg/IBB_5_57830_004v.jpg]] [[File:file_icon.gif|link=http://www.ub.unibas.ch/digi/a100/diverse_projekte/bernoulli-jpg/IBB_5_57830_005r.jpg]] [[File:file_icon.gif|link=http://www.ub.unibas.ch/digi/a100/diverse_projekte/bernoulli-jpg/IBB_5_57830_005v.jpg]] [[File:file_icon.gif|link=http://www.ub.unibas.ch/digi/a100/diverse_projekte/bernoulli-jpg/IBB_5_57830_006r.jpg]] [[File:file_icon.gif|link=http://www.ub.unibas.ch/digi/a100/diverse_projekte/bernoulli-jpg/IBB_5_57830_006v.jpg]]
+[[File:file_icon.gif|link=http://www.ub.unibas.ch/digi/bez/bernoullibriefe/jpg/bernoulli-jpg/BAU_5_000057830_003v.jpg]] [[File:file_icon.gif|link=http://www.ub.unibas.ch/digi/bez/bernoullibriefe/jpg/bernoulli-jpg/BAU_5_000057830_004r.jpg]] [[File:file_icon.gif|link=http://www.ub.unibas.ch/digi/bez/bernoullibriefe/jpg/bernoulli-jpg/BAU_5_000057830_004v.jpg]] [[File:file_icon.gif|link=http://www.ub.unibas.ch/digi/bez/bernoullibriefe/jpg/bernoulli-jpg/BAU_5_000057830_005r.jpg]] [[File:file_icon.gif|link=http://www.ub.unibas.ch/digi/bez/bernoullibriefe/jpg/bernoulli-jpg/BAU_5_000057830_006r.jpg]] [[File:file_icon.gif|link=http://www.ub.unibas.ch/digi/bez/bernoullibriefe/jpg/bernoulli-jpg/BAU_5_000057830_006v.jpg]] [[File:file_icon.gif|link=http://www.ub.unibas.ch/digi/bez/bernoullibriefe/jpg/bernoulli-jpg/BAU_5_000057830_007r.jpg]] [[File:file_icon.gif|link=http://www.ub.unibas.ch/digi/bez/bernoullibriefe/jpg/bernoulli-jpg/BAU_5_000057830_007v.jpg]]
 <!-- End Transkription -->

1720-05-01 Wolff Christian-Bernoulli Johann I: Unterschied zwischen den Versionen

Aktuelle Version vom 20. Juni 2017, 07:16 Uhr

Fussnoten

Navigationsmenü

Suche